创建网格体
3D 场景中所有可视的物体都是网格体。不同的网格体具有不同的形状。在之前的教程中,我们创建过矩形平面,立方体,球形网格体等面状网格体,也创建过坐标轴等线状网格体。这一节,我们将进一步了解,如何创建不同形状的网格体。
基础几何网格体
基础几何网格体包括:矩形平面,立方体,球体,圆柱体,圆锥体。之前的教程中,我们创建过矩形平面和立方体。接下来,我们看看如何创建球体,圆柱体和圆锥体。
- 使用
MeshBuilder.createSphere(scene, radius, widthSegs, heightSegs)创建球体。 - 使用
MeshBuilder.createCylinder(scene, radius, height, segs)创建圆柱体。 - 使用
MeshBuilder.createCone(scene, radius, height, segs)创建圆锥体。
创建所有网格体时,都需要指定当前场景。创建球体时,需要指定球体的半径;创建圆柱和圆锥时,不仅需要指定半径(圆柱或圆锥的底面半径),还需要指定高度。

这几种网格体的表面包含曲面,G3D 是通过短折线来模拟曲线的。比如,一个圆形,可以用 6 段短直线段来粗糙地模拟,也可以用 128 条短直线段来精细地模拟。上述几个函数的 segs 相关参数即是指定使用多少段直线来模拟一个圆形,数值越大,模拟就约精细(当然性能开销也越大)。

下面这个例子展示了创建球体、圆柱体和圆锥体的方法,以及不同 segs 参数生成的网格体的区别。
例子中创建了三个圆柱体,三个球体,三个圆锥体,segs 分别是 6,16 和 128。很明显,不同 segs 参数值对对曲面的逼真程度是有显著影响的。
自定义形状的网格体
除了这些预置好的网格体,我们还可以手动生成顶点,然后拼装成自定义形状的网格体。这项工作需要一些小技巧,我们先看一个简单的情形:如何创建自定义的线状网格体(球体,立方体这些属于面状网格体,而之前创建的坐标轴则是线状网格体)。
线状网格体
假设我们需要创建如下图所示的,在 X-Y 平面中的折线,依次经过 (0, 0, 0),(1, 1, 0),(1, 0, 0),(2, 1, 0),(2, 0, 0) 等等。
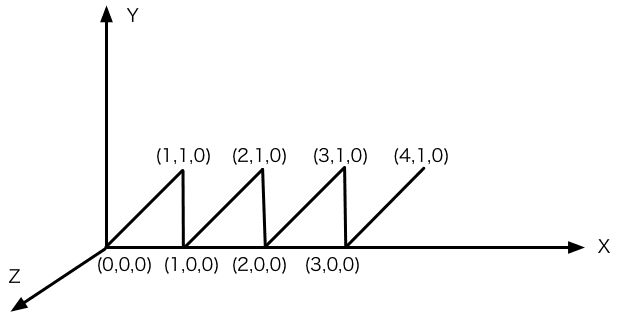
我们看看接下来这个示例是怎么做的。
首先,创建两个数组 vertices 和 indices:
const vertices = [];
const indices = [];
for(let i=0; i<4; i++){
vertices.push(0+i, 0, 0, 1+i, 1, 0);
if(i!==0){
indices.push(i*2-1, i*2);
}
indices.push(i*2, i*2+1);
}
// vertices: [0,0,0, 1,1,0, 1,0,0, 2,1,0, 2,0,0, 3,1,0, ...]
// 0 1 2 3 4 5
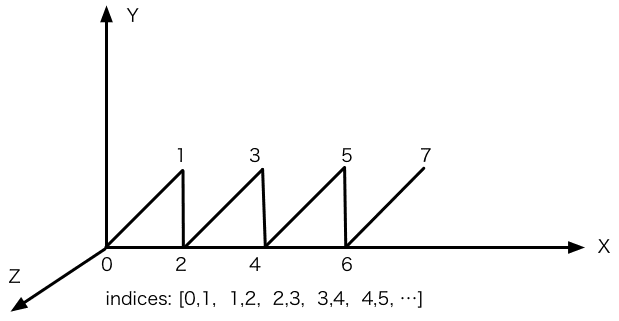
// indices: [0,1, 1,2, 2,3, 3,4, 4,5, ...]数组 vertices 包含了沿折线所有顶点的位置,每三个值表示一个顶点。这个例子中的折线共有 8 个顶点,所以 vertices 的长度是 24。
数组 indices 描述了 vertices 中的顶点是如何构成一条折线的。indices 中的每一个值都是 vertices 中的索引值,都对应了 vertices 中的一个顶点。在这个例子中,indices 是 [0,1,1,2,...]。前两个值 0 和 1 表示:首先,取一根线段,首端是 vertices 中的第 0 个顶点即 (0, 0, 0),尾端是第 1 个顶点即 (1, 1, 0)。接下来的两个值 1 和 2 表示:第二根线段,首端是 vertices 中的第 1 个端点 (1, 1, 0),尾端是第 2 个端点 (1, 0, 0)。首尾相接,依此类推。
然后,就可以新建 LineMesh 即线状网格体对象,然后为其创建一个 LineGeometry 即线状几何体对象,传入 vertices 和 indices 拼成的一个 Config 对象。注意,这里我们将 indices 放在 default 字段中,这是因为一个线状网格体可能包含多条独立的折线,默认第一条折线的名称为 default。
const lines = new G3D.LineMesh(scene);
lines.geometry = new G3D.LineGeometry({
vertices,
indices: {
default: indices
}
})这样,我们就创建了一个自定义形状的线状网格体。
面状网格体
创建面状网格体的过程稍微复杂一点。假设我们想要创建下图中,由两个正方形平面 ABCD 和 EFGH 组成的网格体:
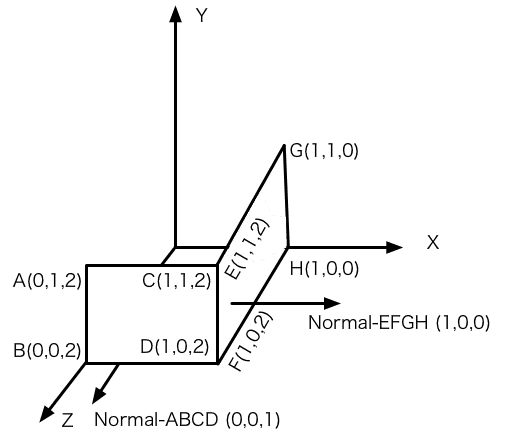
看看示例是怎么做的。
除了顶点数组 vertices 和索引数组 indices,我们还要创建 UV 数组 uvs 和法线数组 normals。
const vertices = [
0,1,2, // A
0,0,2, // B
1,1,2, // C
1,0,2, // D
1,1,2, // E
1,0,2, // F
1,1,0, // G
1,0,0 // H
];
const normals = [];
const uvs = [];
for(let i=0; i<8; i++){
if(i<=3){
normals.push(0,0,1);
}else{
normals.push(1,0,0);
}
uvs.push(0,0);
}顶点数组 vertices 由 8 个顶点组成,这与之前创建线状网格体时的操作是一致的。
法线 normals 是垂直于表面的矢量。对于线状网格体而言,顶点是无所谓法线的,但是对于面状网格体,法线会参与光照的计算,影响最终表面呈现的颜色。所以对面状网格体,法线至关重要。这里,对于前四个顶点,法线为 (0, 0, 1);而对后四个顶点,法线为 (1, 0, 0)。
你也许已经注意到了,其实这个网格体只有 6 个顶点,因为顶点 C 和顶点 E 是同一个顶点,而顶点 D 和顶点 F 也是同一个顶点。但是由于 C 和 E 虽然具有相同的位置,但是法线的值不同,所以不得不将其拆分为两个顶点表示。
UV 与法线类似,也是顶点的属性,但 UV 只需要用两个值来表示。UV 与网格体表面材质上的纹理贴图有关,目前还没有涉及,所以这里为了简单,为每个顶点都指定 UV 为 (0,0) 好了。
最后创建顶点索引数组 indices。在线状网格体中,顶点索引的规则是「每两个点表示一个线段」,而在面状网格体中,规则是「每三个点表示一个三角形」。所有面状网格体都是由三角形组成的,矩形平面需要拆分为两个三角形表达。例子中的 indices 描述了四个三角形,分别是三角形 ABC 与 BDC(它们构成了矩形平面 ABCD),以及三角形 EFH 和 HGE(它们构成了矩形平面 EFGH)。
const indices = [
0,1,2, // triangle ABC
1,3,2, // triangle BDC
4,5,7, // triangle EFH
7,6,4 // triangle HGE
]最后,利用上面生成的这些数组来创建 Mesh 对象。之前构建线状网格体时,我们使用了 LineMesh 和 LineGeometry;此时我们构建面状网格体,需要使用 Mesh 和 Geometry。同样,indices 数组放在了 default 属性中。
const mesh = new G3D.Mesh(scene);
mesh.geometry = new G3D.Geometry({
vertices,
normals,
uvs,
indices: {
default: indices
}
});接下来,请在示例右侧显示区域拖拽鼠标,把相机转到这两个矩形平面的背后去(或者,你也在代码里更改相机的属性,camera.alpha = 200)。你会发现,当相机转到平面背后时,矩形平面消失了!(但是通过 MeshBuilder.createPlane() 方法创建的平面不会这样)。
这是因为,通常情况下,面状网格体是闭合的,你不应该看到一个平面的背面,为了提高性能,默认是不渲染背面的。在 G3D 中,Geomtry 对象具有朝向 (facing) 的概念,在初始化 Geometry 对象时,可以指定一个 facing 属性,可以将其指定为 Geometry.FACING.FRONT(这是默认值),Geometry.FACING.BACK 或 Geometry.FACING.BOTH。
如果我们希望矩形平面的两侧都可以被看到,那么在初始化时传入 BOTH 即可,如下所示。
mesh.geometry = new G3D.Geometry({
...
facing: G3D.Geometry.FACING.BOTH
})如何区分一个平面的正面和背面呢?这时又要用到右手螺旋法则了。拿出右手,使除了大拇指外的四个手指,沿着三角形三个顶点的排列顺序旋转(比如 A->B->C),此时大拇指指向的方向的就是这个平面的「正面」(front)。
小结
这一节,我们学习了两点:1) 如何通过 MeshBuilder 的工厂函数创建具有内置形状的网格体;2) 如何根据实际场景创建自定义形状的网格体。希望能够对你有所帮助。


